Всё, что движется. Прогулки по беспокойной Вселенной от космических орбит до квантовых полей - [139]
. Если для начала представить себе одномерное движение, то возможностей для шагов только две: вправо или влево. На рис. 9.2 это вверх и вниз; там показаны приключения не одного, а трех блуждателей – просто для того, чтобы увидеть сразу несколько. Удаление блуждателей от места старта выражается в том, высоко или низко проходит соответствующая линия на рисунке. Вдоль горизонтальной оси отложено 5000 шагов. Для построения я использовал генератор (псевдо)случайных чисел, а в литературе к делу часто привлекается пьяница, который не может вспомнить, вправо или влево по улице ему надо двигаться, делает шаг наугад, падает, а когда поднимается, не помнит, в какую сторону он только что пытался идти, и снова делает шаг наугад. Для человека здесь труднее всего не падать и подниматься, а делать шаги по-настоящему случайно.
Рис. 9.2. Три реализации случайных блужданий «вверх-вниз» из 5000 шагов. На каждом шаге выполняется смещение на единицу вверх или на единицу вниз. Количество сделанных шагов («время») отложено по горизонтальной оси, а смещение от начальной точки – по вертикальной
Случайность блужданий без памяти имеет свои законы. Эти законы не могут ничего сказать про одного конкретного блуждателя: его приключения на то и случайны (хотя мы и не ожидаем всерьез, что он сделает миллион шагов подряд в одном и том же направлении). Но, представляя себе, что блуждателей много или даже что один и тот же энтузиаст проделывает подобное упражнение каждый вечер, вполне разумно интересоваться их судьбой в среднем. Если на расстоянии 30 шагов вправо по улице находится автобусная остановка и, единожды дойдя до нее, незадачливый персонаж останется там ждать автобуса, то как долго в среднем ему придется ходить туда-сюда, чтобы все-таки оказаться у остановки? Можно спросить и наоборот: на каком максимальном расстоянии от места старта побывает – скорее всего, побывает – блуждатель, если сделает 100 шагов? А если сделает 1000? При блужданиях в двух измерениях – по плоскости – аналогичный вопрос задается про время/число шагов, которое требуется, чтобы выйти из круглого парка. Примеры блужданий в двух измерениях показаны на рис. 9.3: это уже не графики отклонения в зависимости от числа шагов, а сами траектории случайных блуждателей на плоскости. На левом рисунке три блуждателя начинают из одной и той же точки; в каждый момент времени 0, 1, 2, 3, … каждый из них случайным образом выбирает направление и делает шаг длины 1. Общее свойство броуновских блужданий, вне зависимости от числа измерений, выражается в том, насколько далеко с течением времени уходят блуждатели. Ответ: максимальное достигнутое удаление от начала в среднем пропорционально квадратному корню из времени. Точнее, это квадратный корень, умноженный еще на некоторое число – оно важно для реального броуновского движения, но в нашей простой модели равно единице. Сделав 100 шагов, наш блуждатель удалится в среднем на 10 шагов от начала, а сделав 225 шагов – на 15 шагов от начала. Уйти далеко оказывается не самой простой задачей: понадобится (в среднем) совершить 10 000 шагов, чтобы (в среднем!) достичь удаления в 100 шагов от начала. Конечно, чтобы общие закономерности восторжествовали, может понадобиться довольно долгое хождение. Для реализаций, приведенных на рис. 9.3 слева, например, оказалось, что один из блуждателей за 300 сделанных им шагов не ушел далеко от центра, а двое других проявили себя активнее (и по случайности все они разошлись в разных направлениях; вообще-то 300 шагов – это очень мало). Тем не менее при большом числе испытаний получается та самая картина квадратного корня из времени. Это совсем не похоже на движение тел, как мы его знаем: движение с постоянной скоростью означает, что расстояние растет так же, как и время: в три раза дольше означает в три раза дальше. В окружении же «раздробленного» движения, передающего блуждателю случайные пинки, требуется прождать в девять раз дольше, чтобы (в среднем!) получилось в три раза дальше[165].
Рис. 9.3. Траектории случайных блужданий на плоскости. Длина каждого шага равна 1. Слева: три блуждания по 300 шагов каждое. Справа: случайное блуждание в 5000 шагов
Одна проблема с пинками, которые маленький «предмет» получает от молекул, оставалась нерешенной до начала XX в., – это несоответствие масштабов. Размер пыльцы (и, видимо, «крошечных осколков египетского Сфинкса») – около одного микрона, т. е. 10>–4 см, а характерный размер молекулы воды, как мы сейчас знаем, 10>–8 см, т. е. в 10 000 раз меньше (сами броуновские частицы видны в микроскоп, а молекулы/атомы нет). Даже при отсутствии ясных данных о размере атомов и молекул было понятно, что они много меньше, чем частицы, которым они передают свое движение. Кроме того, число столкновений, которые молекула испытывает каждую секунду (скажем, 10>12 в воде), никак не соответствует возможностям человеческого глаза, который способен замечать движение лишь в интервале не менее 1/30 секунды (и микроскоп здесь ничем не поможет). Ответ появился в статье Эйнштейна, вышедшей в мае 1905 г. – примерно за месяц до статьи о теории относительности. Наблюдаемые смещения броуновской частицы – это итог сложения множества одиночных воздействий. Из механизма случайных блужданий удалось вывести, что все то огромное количество элементарных столкновений, которые претерпевает броуновская частица, приводит к ее среднему смещению на несколько микрон при времени наблюдения порядка минуты. Для того чтобы в моей модели на рис. 9.3 описать нечто похожее на
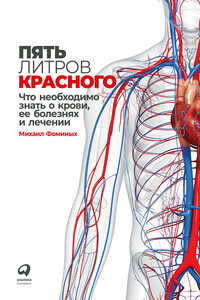
Гематолог-онколог Михаил Фоминых доступным языком рассказывает об анатомии и физиологии крови и кроветворных органов, наиболее часто встречающихся синдромах и заболеваниях системы крови, методах диагностики и лечения, о современной теории канцерогенеза, причинах развития онкологических заболеваний, развенчивает распространенные мифы о крови и ее болезнях. Эта книга содержит важные сведения, которые помогут вам более осознанно и уверенно общаться с врачами, однако ее цель – не только рассказать о возможностях диагностики и лечения гематологических заболеваний, но и расширить наши познания о крови – жизненно важной и необыкновенно интересной жидкой ткани организма.

С самого возникновения цивилизации человечество сосуществует с невидимыми и смертоносными врагами – вирусами. Оспа унесла больше жизней, чем все техногенные катастрофы и кровопролитнейшие войны XX века; желтая лихорадка не позволила Наполеону создать колониальную империю и едва не помешала строительству Панамского канала. Ученый-вирусолог, профессор Майкл Олдстоун, основываясь на свидетельствах современников ужасных эпидемий и ученых, «охотников за микробами», показывает, насколько глубоко влияние вирусов на жизнь человечества.

Билл Най — инженер, телеведущий популярных научных передач («Билл Най — научный парень») и директор Планетарного общества, занимающегося исследованиями в области астрономии и освоения космоса, а также популяризации науки. В своей книги об эволюции он увлекательно, с юмором, рассказывает о происхождении жизни, появлении новых видов, о дарвиновской теории и свидетельствах ее достоверности, которые мы можем найти в окружающей нас жизни, а также о последних исследованиях в медицине, биологии и генной инженерии.

Последняя египетская царица Клеопатра считается одной из самых прекрасных, порочных и загадочных женщин в мировой истории. Её противоречивый образ, документальные свидетельства о котором скудны и недостоверны, многие века будоражит умы учёных и людей творчества. Коварная обольстительница и интриганка, с лёгкостью соблазнявшая римских императоров и военачальников, безумная мегера, ради развлечения обрекавшая рабов на пытки и смерть, мудрая и справедливая правительница, заботившаяся о благе своих подданных, благородная гордячка, которая предпочла смерть позору, — кем же она была на самом деле? Специалист по истории мировой культуры Люси Хьюз-Хэллетт предпринимает глубокое историческое и культурологическое исследование вопроса, не только раскрывая подлинный облик знаменитой египетской царицы, но и наглядно демонстрируя, как её образ менялся в сознании человечества с течением времени, изменением представлений о женской красоте и появлением новых видов искусства.

«Быки» и «медведи» — так называются спекулянты, играющие соответственно на повышении и понижении курса ценных бумаг. Фондовая биржа и является тем местом, где скрещивают копья эти спекулянты-профессионалы. Анализируя механизм биржевой спекуляции, закономерности курсов ценных бумаг, кандидат экономических наук В. П. Федоров показывает социально-экономическую роль биржи, обнажает паразитизм биржевиков, царящую там обстановку узаконенного грабежа и прямой преступности. Работа написана популярно и доступна самому широкому кругу читателей.

Воздушную оболочку Земли — атмосферу — образно называют воздушным океаном. Велик этот океан. Еще не так давно люди, живя на его дне, почти ничего не знали о строении атмосферы, о ее различных слоях, о температуре на разных высотах и т. д. Только в XX веке человек начал подробно изучать атмосферу Земли, раскрывать ее тайны. Много ярких страниц истории науки посвящено завоеванию воздушного океана. Много способов изыскали люди для того, чтобы изучить атмосферу нашей планеты. Об основных достижениях в этой области и рассказывается читателю в нашей небольшой книге.