Правила счета элементов бесконечного множества - [3]
С другой стороны, мы можем проделать то же самое и с четными числами, например, получив в результате, что их в общем ряду только треть. Иначе говоря, один и тот же метод показывает, что среди целых чисел нечетных одновременно только половина и только две трети. Понятно, что методика, дающая два взаимоисключающих результата не вызывает доверия.
Группировка степеней. Такие методики пересчета, отождествления всегда содержат плохо скрытую подмену понятий. Например, с рядом натуральных чисел отождествляется ряд степеней 10>1, 10>2, 10>3 … 10>n… и так далее. Таким же образом устанавливается взаимно однозначное соответствие и между множеством натуральных чисел и множеством всех квадратов натуральных чисел 1>2, 2>2, 3>2, … n>2… и так далее. Но принять такое отождествление нет никаких оснований.
Нужно просто обратить внимание на то, что же именно отождествляется. В обоих приведенных примера сразу же можно заметить присутствие члена натурального ряда. Понятно, что отождествляются не значения членов ряда, а их порядковые номера, которые самым наглядным образом обозначены в каждом из членов рядов. До начала отождествления каждый член ряда уже имеет свой натуральный порядковый номер, а значение самого члена ряда не имеет никакого смысла. Это могут быть и летучие обезьяны с соответствующей биркой на шее, и протоны в бесконечной Вселенной, которые ещё только предстоит пометить соответствующим номером, и даже множество миров Эверетта.
Группировка в пары. Попробуем теперь просто пересчитать, перенумеровать все натуральные числа, предварительно соединив их в пары четное-нечетное число: (1,2), (3,4), (5,6), то есть, присваивая каждой паре последовательно номера 1, 2, 3, 4 и так далее. Очевидно, что каждой паре будет присвоен один номер, натуральное число. И мы получаем явное противоречие, поскольку это означает, что количество всех натуральных чисел, собранных в пары, в два раза больше количества всех натуральных чисел. Буквально, количество всех натуральных чисел в два раза больше количества всех натуральных чисел. Но натуральные числа можно группировать и тройками, пятерками, десятками и так далее.
Десять рядов. Еще более наглядно подмена понятий будет видна, если составить из натурального ряда десять новых рядов, каждый из которых содержит натуральные числа, оканчивающиеся на 0, 1, 2 и так далее до 9. Если теперь пересчитать их количества, то для каждого ряда, как и в случае (1) мы получим количество, совпадающее с количеством натуральных чисел. Теперь вновь соединим все эти ряды в единый. Очевидно, что в результате мы получим исходный ряд – натуральные числа. Получается, что количество членов просуммированного ряда в десять раз больше, чем в ряду натуральных чисел. Но ведь просуммированный ряд – это тот же самый натуральный ряд. Здесь совершается та же ошибка: подсчет без учета принадлежности чисел выделенных рядов исходному, натуральному ряду.
Квадратная таблица. Однако и это не предел. Можно, например, составить таблицу из n строк натуральных чисел, поэтому, соответственно, столбцов будет тоже n, где n – натуральное число. Теперь подсчитаем, перенумеруем диагональным процессом Кантора все числа этой таблицы. Очевидно, что каждое из чисел получит свой порядковый номер, которых, понятно, будет ровно n, стремящееся к бесконечности. Но таблица определенно содержит n>2 элементов. Получается, что количество n>2 элементов равно n, или, другими словами, количество всех натуральных чисел равно квадрату количества всех натуральных чисел. Конечно, сами натуральные числа к этому непричастны. Проблему создаёт выбор специфических способов подсчета, в основе которых явно лежат методы Кантора, позволяющие получить любой, произвольный результат. Поскольку один и тот же метод при корректном применении даёт разные результаты, такой метод не может быть верным.
О счетности континуума – точек на отрезке
Как утверждается со ссылкой на методологию счета Кантора, множество всех действительных чисел несчетно, то есть, невозможно их пересчитать, присвоив каждому из них некоторое натуральное число – номер, поскольку всегда останутся непронумерованные числа [3, с.73-74]. Вообще-то, на первый взгляд, интуитивно это выглядит вполне очевидно. Рассмотрим, например, следующую явно бесконечную последовательность действительных чисел:
В этих числах запятая просто занимает позицию n, представляющую натуральное число, поэтому чисел в указанной последовательности в точности равно числу строк, n, где n равно бесконечности. Поскольку все номера натуральных чисел использованы для нумерации этих действительных чисел, то очевидно, что остальное множество действительных чисел осталось без номеров, то есть их множество – несчетно. В связи с хитростями нумерации, как правило, вспоминают математика Кантора, который, как считается, доказал, что число точек на отрезке прямой сосчитать никаким способом нельзя. Утверждается, что их нельзя перенумеровать с помощью бесконечного ряда натуральных чисел, приписывая каждой точке свой номер, в каком бы порядке мы ни выбирали эти точки. Всегда останется хотя бы одна точка, на которую не хватит номера!

Рассмотрена модификация традиционной установки для телепортации квантового состояния кубита. На передающей стороне изменена на противоположную последовательность гейтов CNOT и гейта Адамара. Модифицированная установка позволяет телепортировать теперь уже не просто неизвестное состояние кубита, а состояние запутанности кубитов. На стороне передатчика установка переводит два кубита в состояние запутанности, в результате чего и на стороне приемника два кубита также оказываются в состоянии запутанности. Показана также возможность непосредственной сверхсветовой передачи классической информации с помощью гейта CNOT.
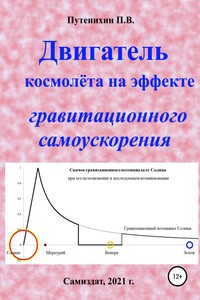
Считается, что для разгона космического корабля до больших, вплоть до субсветовых, скоростей необходимы значительные запасы топлива. Однако ограниченность скорости распространения гравитации приводит к возникновению релятивистского эффекта гравитационного самоускорения, когда протяженный объект увеличивает скорость своего движения без приложения к нему внешней силы, так называемое, безопорное движение. Spacecraft engine on the effect of gravitational self-acceleration It is believed that significant reserves of fuel are required to accelerate a spacecraft to high speeds, up to subluminal speeds.

Истинное православие весьма отличается от его расхожих версий, излагаемых в благоглупостных книжках о вере и церкви. Оно почти недоступно не только наблюдению, но даже словесному описанию. Однако не все так плохо. Нужно просто отойти чуть в сторону от тех смотровых площадок, откуда православие обычно — и безуспешно — показывают, и обратиться к историческим и современным прецедентам христианского бытия, когда оно направлено «против течения» нехристианской или псевдохристианской общественной жизни. Может ли адекватный современный человек быть православным? Кто такие истинные верующие? Каковы настоящие христианские ценности? В чем подлинный смысл церковной жизни? Эта книга раскрывает совершенно неожиданные и удивительные стороны жизни христианина.

Вопрос мифического (мистического) в нашей жизни сейчас встаёт всё острее. Люди хотят знать объективную реальность и научиться воспринимать её адекватно. В книге внимание уделено механизмам самого мифотворчества. Изучена роль языка как описательной силы при создании картины мира. Показано, как неадекватные языковые конструкции создают и неадекватную картину реальности. С позиций психолингвистики, язык – это инструмент описания и орудие мышления, поэтому для начала нужно разобраться в самих орудиях и их силе.

Небольшие эссе, из которых составлен данный сборник, написаны самыми известными учеными и мыслителями наших дней, участниками научно-просветительского проекта Edge.org. На этот раз великолепная «команда знатоков» подвергает ревизии само устройство научной деятельности. Почему некоторые устаревшие идеи и концепции по-прежнему находятся в научном обиходе?Как и можно предположить, ответы оказались весьма разнообразными и подчас неожиданными: по мнению ведущих профессионалов современной науки, немедленного пересмотра заслуживают не только многие теории, но и краеугольные принципы самого́ научного подхода…

Прививки могут стать причиной аутизма, серьезные болезни лечатся гомеопатией, ВИЧ неизбежно приводит к смерти, ГМО опасно употреблять в пищу — так ли это? Знать верный ответ важно каждому, ведь от этого зависят наша жизнь и здоровье. В своей новой книге научный журналист Ася Казанцева объясняет: чтобы разобраться, достоверно ли то или иное утверждение, необязательно быть узким специалистом. Главное — научиться анализировать общедоступную информацию. И тогда, если «в интернете кто-то неправ», вы это обязательно заметите.Первую книгу Аси Казанцевой «Кто бы мог подумать? Как мозг заставляет нас делать глупости» высоко оценили ученые и обычные читатели — уже несколько лет она остается бестселлером.

Известный телеведущий Игорь Прокопенко в своей книге раскрывает материалы, которые до сегодняшнего дня находились в архивах спецслужб под грифом «Совершенно секретно».Вы узнаете о том, как спецслужбы разных стран разрабатывают теорию и практику массового зомбирования людей; как готовят специалистов-«слиперов», которые могут, находясь за тысячи километров, войти в сознание, например, министра обороны враждебной державы.Мы познакомимся с уникальными экспериментами секретных лабораторий, где экстрасенсы занимаются телекинезом и ясновидением.

Игорь Прокопенко в своей книге приводит ранее неизвестные документальные факты и свидетельства участников и очевидцев Чеченской войны. Автор заставляет по-новому взглянуть на трагические события той войны. Почему с нашей страной случилась такая страшная трагедия? Почему государством было сделано столько ошибок? Почему по масштабам глупости, предательства, коррупции и цинизма эта война не имела себе равных? Главными героями в той войне, по мнению автора, стали простые солдаты и офицеры, которые брали на себя ответственность за принимаемые решения, нарушая устав, а иногда и приказы высших военных чинов.